THE SIMPLEST KALMAN FILTER IN THE WORLD
Jack Mo
INTRODUCTION
Kalman filter is the optimal information processor in zero-mean gaussian pdf conditions. It makes use of a key feature of the gaussian distribution family: the product of two gaussian function is another gaussian function. The process to multiply two GDFs (gaussian distribution functions) together is also called data fusion.
THE FUSION OF TWO DATA SOURCES IN ONE DIMENSION
Suppose we have two temperature sensors whose measurements are both noisy and gaussian, then we can describe them use two GDFs.
![]() (1)
(1)
![]() (2)
(2)
The fusion function is given by the product of ![]() and
and ![]() .
.
![]() (3)
(3)
The quadratic terms in this new function can be expanded and then the whole expression can be rewritten to be a new GDF
![]() (4)
(4)
where
![]() (5)
(5)
![]() (6)
(6)
IMPLEMENTING THE SIMPLEST KALMAN FILTER
One thing should be pointed out is that the information we combine together does not necessarily come from measurements. As a matter of fact, in most of the cases we always have some previous knowledge about the system and we can predict how it will change according to the current state. For example, imagine we are in a moving train. With current position and speed given, we can approximately predict where the train will be in the next few seconds. But we are not so sure about our prediction, because we don’t know whether the driver will take an acceleration or a break during the period. That is to say, our prediction is noisy too. Consider it’s gaussian, then we can fuse it with sensor measurements. Here below, I just implemented a basic kalman filter that can be the easiest one in the world. It fuses current prediction and measurement together, and produces an estimation of the most probable state.
File: kalman.h
/* file: kalman.h */
#ifndef __KALMAN_H__
#define __KALMAN_H__
#ifdef __cplusplus
extern "C" {
#endif
#include
#include
#include
typedef struct Kalman
{
/* Critical Section */
float q; // process noise
float r; // measurement noise
/* Critical Section */
float e; // estimation
float d; // difference
float k; // kalman gain
float p; // fused variance
}Kalman;
struct Kalman* KalmanCreate();
void KalmanReset(struct Kalman* kalman);
void KalmanSetE(struct Kalman* kalman, float e);
void KalmanSetD(struct Kalman* kalman, float d);
void KalmanSetQ(struct Kalman* kalman, float q);
void KalmanSetR(struct Kalman* kalman, float r);
float KalmanFilter(struct Kalman* kalman, float x);
void KalmanDestroy(struct Kalman* kalman);
#ifdef __cplusplus
}
#endif
#endif
File: kalman.c
/* file: kalman.c */
#include "kalman.h"
#define SQR(x) (x*x)
struct Kalman* KalmanCreate()
{
Kalman* kalman = (Kalman*)malloc(sizeof(Kalman));
if (kalman == NULL) return NULL;
KalmanReset(kalman);
return kalman;
}
void KalmanReset(struct Kalman* kalman)
{
kalman->e = 0;
kalman->d = 0;
kalman->k = 0;
kalman->p = 0;
}
void KalmanSetE(struct Kalman* kalman, float e)
{
kalman->e = e;
}
void KalmanSetD(struct Kalman* kalman, float d)
{
kalman->d = d;
}
void KalmanSetQ(struct Kalman* kalman, float q)
{
kalman->q = q;
}
void KalmanSetR(struct Kalman* kalman, float r)
{
kalman->r = r;
}
float KalmanFilter(struct Kalman* kalman, float x) {
// update
kalman->e += kalman->d;
kalman->p += kalman->q;
// fusion
kalman->k = kalman->p / (kalman->p + kalman->r); // kalman gain
kalman->d = (x - kalman->e) / kalman->k; // delta mean
kalman->e += kalman->d; // fused mean
kalman->p -= kalman->p * kalman->k; // fused variance
return kalman->e;
}
void KalmanDestroy(struct Kalman* kalman)
{
if (kalman != NULL) {
free(kalman);
kalman = NULL;
}
}
PREVIOUS JOB TO DO BEFORE USING OUR KALMAN FILTER
In the implementation above, two parameters must be known before the filter process is actually put into use. One is the process noise, which is the uncertainty comes from the prediction step, the other is measurement noise, which is the uncertainty comes from the sensor. The former can be assigned a reasonable one, according to the system itself. The latter should be tested out carefully. To accomplish this, I wrote another helper functions which can calculate various of statistic features all together.
File: gauss.h
/* file: gauss.h */
#ifndef __GAUSS_H__
#define __GAUSS_H__
#ifdef __cplusplus
extern "C" {
#endif
#include
#include
#include
typedef struct Gauss
{
/* Critical Section */
uint16_t N; // buffer length
/* Critical Section */
float* buf; // buffer
uint16_t n; // initialization counter
uint16_t i; // current enqueuing buffer index
float sum; // sum of buffer
float diff; // diff of sum
float res0; // residual of the number 0 parameter
float resn; // residual of the number (n - 1) parameter
float mean; // mean of buffer
float last_mean; // last mean
float delta_mean; // delta of mean
float sse; // sum of square error
float delta_sse; // delta of sse
float mse; // mean square error
float last_mse; // last mse
float delta_mse; // delta mse
}Gauss;
struct Gauss* GaussCreate(uint16_t N);
void GaussReset(struct Gauss* gauss);
float GaussFilter(struct Gauss* gauss, float x);
void GaussDestroy(struct Gauss* gauss);
#ifdef __cplusplus
}
#endif
#endif
File: gauss.c
/* file: gauss.c */
#include "gauss.h"
#define SQR(x) (x*x)
struct Gauss* GaussCreate(uint16_t N)
{
Gauss* gauss = (Gauss*)malloc(sizeof(Gauss));
if (gauss == NULL) return NULL;
gauss->buf = (float*)malloc(N * sizeof(float));
if (gauss->buf == NULL) {
free(gauss);
gauss = NULL;
return NULL;
}
gauss->N = N;
GaussReset(gauss);
return gauss;
}
void GaussReset(struct Gauss* gauss)
{
memset(gauss->buf, 0, gauss->N * sizeof(float));
gauss->n = 0;
gauss->i = 0;
gauss->sum = 0;
gauss->diff = 0;
gauss->res0 = 0;
gauss->resn = 0;
gauss->mean = 0;
gauss->last_mean = 0;
gauss->delta_mean = 0;
gauss->sse = 0;
gauss->delta_sse = 0;
gauss->mse = 0;
gauss->last_mse = 0;
gauss->delta_mse = 0;
}
float GaussFilter(struct Gauss* gauss, float x) {
gauss->last_mean = gauss->mean;
gauss->last_mse = gauss->mse;
if (gauss->n < gauss->N) {
gauss->buf[gauss->n++] = x;
gauss->sum += x;
gauss->mean = gauss->sum / gauss->n;
gauss->delta_mean = gauss->mean - gauss->last_mean;
gauss->resn = x - gauss->mean;
gauss->sse += SQR(gauss->resn);
gauss->mse = gauss->sse / gauss->n;
gauss->delta_mse = gauss->mse - gauss->last_mse;
} else {
if (gauss->i == gauss->N) gauss->i = 0;
gauss->diff = x - gauss->buf[gauss->i];
gauss->sum += gauss->diff;
gauss->mean = gauss->sum / gauss->n;
gauss->delta_mean = gauss->mean - gauss->last_mean;
gauss->res0 = gauss->buf[gauss->i] - gauss->last_mean;
gauss->resn = x - gauss->mean;
gauss->delta_sse = (gauss->diff) * (gauss->resn + gauss->res0);
gauss->sse += gauss->delta_sse;
gauss->mse = gauss->sse / gauss->n;
gauss->delta_mse = gauss->mse - gauss->last_mse;
gauss->buf[gauss->i++] = x;
}
return gauss->mean;
}
void GaussDestroy(struct Gauss* gauss)
{
if (gauss != NULL) {
if (gauss->buf != NULL) {
free(gauss->buf);
gauss->buf = NULL;
}
free(gauss);
gauss = NULL;
}
}
USE OUR KALMAN FILTER IN AN INTEL CRURIE BOARD
To make our kalman filter take real effect and verify it’s performance, we must get it run. I happen to have an arduino101 board with an intel crurie core inside on hand. Other than most of the arduino boards, the arduino101 board integrates a 6-axis imu, so I decide to make use of it. I use the kalman filter implemented above to smooth the acceleration in x-axis. The code is directly modified from the samples given by the arduino IDE. To protect copyright, the notice is included. Hope it’ll not bother you.
File: CrurieIMUKalman.ino
/* file: CrurieIMUKalman.ino */
/*
===============================================
Example sketch for CurieIMU library for Intel(R) Curie(TM) devices.
Copyright (c) 2015 Intel Corporation. All rights reserved.
Based on I2C device class (I2Cdev) demonstration Arduino sketch for MPU6050
class by Jeff Rowberg: https://github.com/jrowberg/i2cdevlib
===============================================
I2Cdev device library code is placed under the MIT license
Copyright (c) 2011 Jeff Rowberg
Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files (the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in
all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.
===============================================
*/
#include "CurieIMU.h"
#include "gauss.h"
#include "kalman.h"
int ax, ay, az; // accelerometer values
int gx, gy, gz; // gyrometer values
const int ledPin = 13; // activity LED pin
boolean blinkState = false; // state of the LED
int calibrateOffsets = 1; // int to determine whether calibration takes place or not
#define GAUSS_N 100
Gauss* gauss = NULL;
Kalman* kalman = NULL;
void setup() {
Serial.begin(9600); // initialize Serial communication
while (!Serial); // wait for the serial port to open
if (gauss == NULL) {
gauss = GaussCreate(GAUSS_N);
if (gauss == NULL) {
Serial.println("GaussCreate() returned NULL, system pending.");
while(1);
} else {
Serial.println("GaussCreate() done.");
}
}
if (kalman == NULL) {
kalman = KalmanCreate();
if (kalman == NULL) {
GaussDestroy(gauss);
Serial.println("KalmanCreate() returned NULL, system pending.");
while(1);
} else {
Serial.println("KalmanCreate() done.");
}
}
// initialize device
Serial.println("Initializing IMU device...");
CurieIMU.begin();
// verify connection
Serial.println("Testing device connections...");
if (CurieIMU.begin()) {
Serial.println("CurieIMU connection successful");
} else {
Serial.println("CurieIMU connection failed");
}
// use the code below to calibrate accel/gyro offset values
if (calibrateOffsets == 1) {
Serial.println("Internal sensor offsets BEFORE calibration...");
Serial.print(CurieIMU.getAccelerometerOffset(X_AXIS));
Serial.print("\t"); // -76
Serial.print(CurieIMU.getAccelerometerOffset(Y_AXIS));
Serial.print("\t"); // -235
Serial.print(CurieIMU.getAccelerometerOffset(Z_AXIS));
Serial.print("\t"); // 168
Serial.print(CurieIMU.getGyroOffset(X_AXIS));
Serial.print("\t"); // 0
Serial.print(CurieIMU.getGyroOffset(Y_AXIS));
Serial.print("\t"); // 0
Serial.println(CurieIMU.getGyroOffset(Z_AXIS));
// To manually configure offset compensation values,
// use the following methods instead of the autoCalibrate...() methods below
//CurieIMU.setAccelerometerOffset(X_AXIS,495.3);
//CurieIMU.setAccelerometerOffset(Y_AXIS,-15.6);
//CurieIMU.setAccelerometerOffset(Z_AXIS,491.4);
//CurieIMU.setGyroOffset(X_AXIS,7.869);
//CurieIMU.setGyroOffset(Y_AXIS,-0.061);
//CurieIMU.setGyroOffset(Z_AXIS,15.494);
Serial.println("About to calibrate. Make sure your board is stable and upright");
delay(5000);
// The board must be resting in a horizontal position for
// the following calibration procedure to work correctly!
Serial.print("Starting Gyroscope calibration and enabling offset compensation...");
CurieIMU.autoCalibrateGyroOffset();
Serial.println(" Done");
Serial.print("Starting Acceleration calibration and enabling offset compensation...");
CurieIMU.autoCalibrateAccelerometerOffset(X_AXIS, 0);
CurieIMU.autoCalibrateAccelerometerOffset(Y_AXIS, 0);
CurieIMU.autoCalibrateAccelerometerOffset(Z_AXIS, 1);
Serial.println(" Done");
Serial.println("Internal sensor offsets AFTER calibration...");
Serial.print(CurieIMU.getAccelerometerOffset(X_AXIS));
Serial.print("\t"); // -76
Serial.print(CurieIMU.getAccelerometerOffset(Y_AXIS));
Serial.print("\t"); // -2359
Serial.print(CurieIMU.getAccelerometerOffset(Z_AXIS));
Serial.print("\t"); // 1688
Serial.print(CurieIMU.getGyroOffset(X_AXIS));
Serial.print("\t"); // 0
Serial.print(CurieIMU.getGyroOffset(Y_AXIS));
Serial.print("\t"); // 0
Serial.println(CurieIMU.getGyroOffset(Z_AXIS));
}
// configure Arduino LED for activity indicator
pinMode(ledPin, OUTPUT);
}
#define GAUSS_PRECISION 0.5f
#define PROC_NOISE 0.1
bool calied = false;
void loop() {
// read raw accel/gyro measurements from device
CurieIMU.readMotionSensor(ax, ay, az, gx, gy, gz);
// these methods (and a few others) are also available
//CurieIMU.readAcceleration(ax, ay, az);
//CurieIMU.readRotation(gx, gy, gz);
//ax = CurieIMU.readAccelerometer(X_AXIS);
//ay = CurieIMU.readAccelerometer(Y_AXIS);
//az = CurieIMU.readAccelerometer(Z_AXIS);
//gx = CurieIMU.readGyro(X_AXIS);
//gy = CurieIMU.readGyro(Y_AXIS);
//gz = CurieIMU.readGyro(Z_AXIS);
// display tab-separated accel/gyro x/y/z values
/*
Serial.print("a/g:\t");
Serial.print(ax);
Serial.print("\t");
Serial.print(ay);
Serial.print("\t");
Serial.print(az);
Serial.print("\t");
Serial.print(gx);
Serial.print("\t");
Serial.print(gy);
Serial.print("\t");
Serial.println(gz);
*/
if (calied == false) {
if (gauss->n < gauss->N || fabs(gauss->delta_mse) > GAUSS_PRECISION) {
GaussFilter(gauss, ax);
Serial.print("ax:\t");
Serial.print(ax);
Serial.print("\t");
Serial.print(gauss->mean);
Serial.print("\t");
Serial.print(gauss->mse);
Serial.print("\t");
Serial.println(gauss->delta_mse);
} else {
KalmanSetE(kalman, gauss->mean);
KalmanSetD(kalman, gauss->delta_mean);
KalmanSetQ(kalman, PROC_NOISE);
KalmanSetR(kalman, gauss->mse);
calied = true;
GaussDestroy(gauss);
}
}
if (calied) {
KalmanFilter(kalman, ax);
Serial.print("ax:\t");
Serial.print(ax);
Serial.print("\t");
Serial.println(kalman->e);
}
// blink LED to indicate activity
blinkState = !blinkState;
digitalWrite(ledPin, blinkState);
}
TESTING RESULT
The following two pictures show the effectiveness of the kalman filter we implemented above. It’s obvious that the curve looks better when filtered.
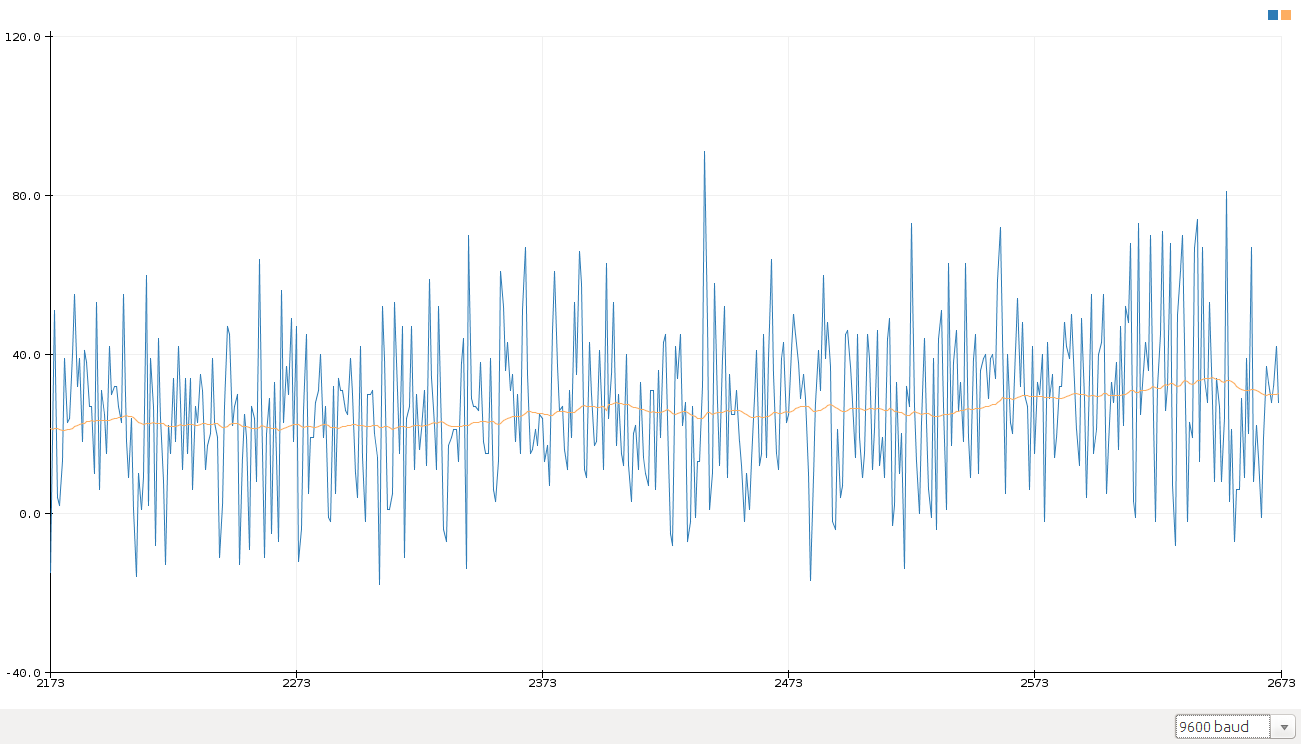 Figure 1.
Figure 1.
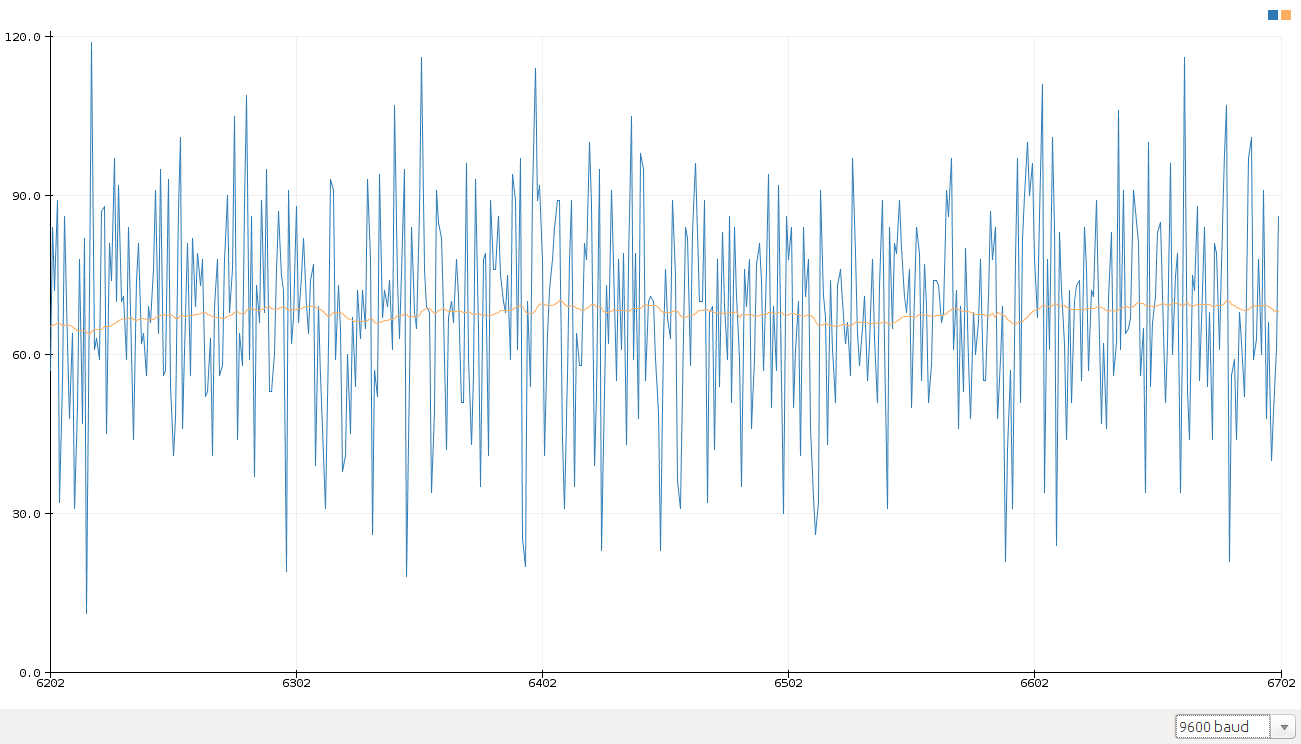
Figure 2.
To observe the filtering result more vividly, click the video below.
The code in this page can be cloned @ github.
More detailed derivation of kalman filter can be refered in this paper.

帮杰
疯狂于web和智能设备开发,专注人机互联。
HOW DO I DIY MY OWN REMOTE CONTROL SWITCH IN MY DORMITORY
THE SIMPLEST KALMAN FILTER IN THE WORLD
COMPUTING MEAN AND VARIANCE RECURSIVELY
LEARNING GOOGLE TENSORFLOW [L1: MAKE THE FIRST ACUAINTANCE]