LIDAR ODOMETRY

 

Jack Mo (mobangjack@whu.edu.cn)

http://twogen.cn

背景

在用激光雷达（LIDAR）做实时定位与地图构建（SLAM）时，不仅需要LIDAR的点云数据，还需要LIDAR的里程计（Odometry）信息。里程计数据可以从其他传感器获得，如IMU的二阶状态估计、电机编码器（Encoder）的角度换算值、其他视觉里程计等。当然，LIDAR本身也可以作为里程计使用。下面我们将以上海思岚科技有限公司（slamtec.com）的RPLIDAR A2为例，讨论用2D LIDAR来获取里程计数据的方法。

LIDAR简介

LIDAR是Light Detection and Range的简写，即“激光探测与测量”。现在常说的LIDAR传感器，大多指激光雷达这一类。图1为RPLIDAR的产品实物图。

（注：本文中所有有关RPLIDAR产品的图表均摘自RPLIDAR的官方数据手册）

图1 RPLIDAR 实物图

LIDAR系统部件

如图2，RPLIDAR主要包含激光测距核心和底座两部分。测距核心包含激光发射器、接收器和微处理器，底座负责供电并驱动激光测距核心绕轴心以一定速率运转。

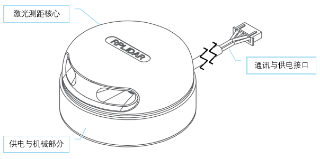
图2 RPLIDAR系统部件

LIDAR工作原理

图3为RPLIDAR的测量原理图。

LIDAR的一个测距周期大致包含以下步骤：

1）发射器发射一束调制过的激光光束；

2）开启内部高精度定时器；

3）光束在遇到障碍物后部分反射到接收器；

4）放大、解调接收到的激光回波；

5）确认是本系统发射出的探测激光，停止内部计时；

6）解算数据。

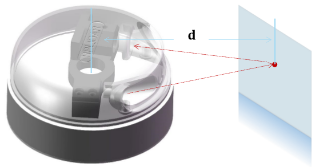
图3 RPLIDAR工作原理

解算后的数据以LIDAR坐标系为参考，包含角度 及距离 。图3为RPLIDAR坐标系示意。

图4 RPLIDAR坐标系

当然，由于系统设计和构造上的原因， 和 也有一定限制。表1为RPLIDAR的性能参数表。由该表可见，RPLIDAR的测距范围最大为6米，最小为0.15米，精度为0.5毫米；角度范围为0~360度，分辨率为0.45度；测量频率2000~4100Hz，扫描频率为5~15Hz。

 

表1 RPLIDAR性能参数表

提取LIDAR里程计数据

LIDAR的每个测量数据包含两个维度的信息，一个是该点与激光雷达的相对方向 ，另一个是该点与激光雷达的径向距离 ，即雷达坐标系采用的是极坐标 。把 当作自变量， 为应变量，雷达一周的扫描数据可以描述为一个映射：

(1)

由于激光雷达具有一定的角度、距离测量范围和分辨率，所以实际的 并非连续。设雷达角度测量范围为 ，分辨率为 ，则

(2)

(3)

(4)

(5)

设雷达距离测量范围为 ，分辨率为 ，则

(6)

(7)

(8)

(9)

所以

(10)

记

(11)

(12)

则激光雷达一个周期的测量数据可以描述为一个集合

(13)

记

(14)

则

(15)

下标k可以表示角度 ，我们把集合中的 去掉，这样，激光雷达一个周期的扫描数据可以描述为一个n维向量x，

(16)

以上面介绍的RPLIDAR为例，

 (17)

 (18)

 (19)

问题：平面内有一点集 ，已知t时刻雷达对X的观测值为 ，t+1时刻雷达对X的观测值为 。求从t时刻到t+1时刻雷达坐标系的旋转 和位移 。（在本文中我们用和t有关的右上标表示数据的时间戳，如 表示t时刻的一组观测数据）

图5 坐标系变换

设t时刻雷达坐标系为 ，t+1时刻雷达坐标系为 ，则 ：

(20)

根据此变换，用 来匹配 ，并计算误差

 (21)

上式隐含了从极坐标到直角坐标的转换，并计算所有待匹配点的欧氏距离。

令

(22)

(23)

得

 

 (24)

最小化匹配误差，从而得到最优变换参数

(25)

将优化后的参数k，l回代(23)(24)可以得到在最小匹配误差下， 的雷达坐标系旋转、平移参数 、 。在直角坐标系下， 分解为 和

(26)

(27)

逐次迭代上面的算法，可以获得LIDAR在任意时刻与初始位姿的相对关系。

总里程

(28)

总偏航

(29)

此外，用上面计算得到的一阶状态量对时间求导还可以得到LIDAR运动的角速度和线速度等信息。

上面虽然假设所使用的的观测数据有时间关系，但式(21)(24)可以脱离该假设使用。对任意两组观测数据 ，定义最小匹配误差

(30)

式(30)可以用来匹配LIDAR扫描过的点，并完善SLAM中的构图。例如剔除不稳定的点或新增之前没扫描到的点。

C++ ROS Node Code

#include "ros/ros.h"
#include "sensor_msgs/LaserScan.h"
#include 
#include 
#include 
#include <sys/time.h>

#define RAD2DEG(x) ((x)*180./M_PI)
#define DEG2RAD(x) ((x)*M_PI/180.)
#define SQUARE(x) ((x)*(x))

int ms()
{
    struct timeval tv;
    gettimeofday( &tv, NULL );
    return tv.tv_sec * 1000 + tv.tv_usec / 1000;
}

void procCallback(const sensor_msgs::LaserScan::ConstPtr& scan)
{
    //int t = ms();
    const int N = 360;
    static float cacher[N] = {0};
    static float stheta = 0.f;
    static float srho = 0.f;
    //static float cachex[N] = {0};
    //static float cachey[N] = {0};
    static int cnt = 0;
    const int CNT = 20;
    const float eps = 1.0f;
    const float lam = 0.03f;
    const float dtheta_max = 50.0f;
    const float dtheta_min = -dtheta_max;
    const float drho_max = 0.2f;
    const float drho_min = -drho_max;
    const int kmax = dtheta_max / eps;
    const int kmin = dtheta_min / eps;
    const int lmax = drho_max / lam;
    const int lmin = drho_min / lam;
    //const int loop = (kmax - kmin) * (lmax - lmin);
    int count = scan->scan_time / scan->time_increment;
    if(cnt < CNT) {
        for(int i = 0; i < count; i++) {
            //float rad = scan->angle_min + scan->angle_increment * i;
            //float range = scan->ranges[i];
            cacher[i] = scan->ranges[i];
            //cachex[i] = range  * cos(rad);
            //cachey[i] = range  * sin(rad);
        }
	cnt++;
    } else {
        float error = FLT_MAX;
        int ke = 0, le = 0;
        for(int k = kmin; k < kmax; k++) {
            for(int l = lmin; l < lmax; l++) {
                float err = 0;
                for(int i = 0; i < count; i++) {
                    int ze = i + k;
                    if(ze < 0) {
                        ze += N;
                    } else if(ze > N - 1) {
                        ze -= N;
                    }
                    if(!std::isnormal(cacher[ze]))
                        continue;
                    float rad = scan->angle_min + scan->angle_increment * i;
                    float range = scan->ranges[i];
                    if(!std::isnormal(range))
                        continue;
                    float xi = range * cos(rad);
                    float yi = range * sin(rad);
                    float re = cacher[ze] + l * lam;
                    float xe = re * cos(rad);
                    float ye = re * sin(rad);
                    float dx = xi - xe;
                    float dy = yi - ye;
                    if(std::isnormal(dx) && std::isnormal(dy))
                        err += SQUARE(dx) + SQUARE(dy);
                }
                if(err < error) {
                    error = err;
                    ke = k;
                    le = l;
                }
            }
        }
        float dtheta = ke * eps;
        float drho = le * lam;
        /*
        float dz = DEG2RAD(dtheta);
        float dx = drho * cos(dz);
        float dy = drho * sin(dz);
        float vx = dx / scan->scan_time;
        float vy = dy / scan->scan_time;
        float vz = dz / scan->scan_time;
        */
        stheta += dtheta;
        srho += drho;

        if(srho < 0)
            srho = 0;

        /*
        float pz = DEG2RAD(stheta);
        float px = srho * cos(pz);
        float py = srho * sin(pz);
        */
        for(int i = 0; i < count; i++) {
            cacher[i] = scan->ranges[i];
        }
        //t = ms() - t;
        ROS_INFO("a=%.2f,r=%.2f,e=%.2f", stheta, srho, error);
        //ROS_INFO("a=%.2f,r=%.2f,da=%.2f,dr=%.2f,dx=%.2f,dy=%.2f,dz=%.2f,px=%.2f,py=%.2f,pz=%.2f,vx=%.2f,vy=%.2f,vz=%.2f,l=%d,t=%d", stheta, srho, dtheta, drho, dx, dy, dz, px, py, pz, vx, vy, vz, loop, t);
    }
}


int main(int argc, char **argv)
{
    ros::init(argc, argv, "rplidar_node_client");
    ros::NodeHandle n;

    ros::Subscriber sub = n.subscribe("/scan", 1000, procCallback);

    ros::spin();

    return 0;
}

 

RPLIDAR官方直接给出了RPLIDAR SDK的ROS集成，为代码编写提供了极大的便利。原理已经在前面叙述，此处代码比较简单，没有添加注释。需要注意的是，为加快求解速度，代码中缩小了参数空间。

算法实测

下面为上述算法在ROS下的实测效果，控制台中a为LIDAR坐标系旋转角度，r为LIDAR坐标系位移，e为相邻兩帧LIDAR扫描数据的sum of error，其他性能参数未给出。测试过程中目测了一番，角度解算比较理想，位移解算与实际情况有较大偏差。

结语

本章我们从LIDAR相邻兩帧数据与坐标系变换的关系出发，通过逐次迭代的方法来获取LIDAR的里程计信息。值得思考的是，在该算法中我们只关注了这兩帧数据之间的关系，并没有考虑一帧数据本身的结构或特征，下一章我们将讨论如何将更多的信息利用起来，让我们的算法更加robust。